¿Qué es el dominio de una función?

El dominio de una función Df= R es el conjunto de todos los valores de la variable independiente Df= R para los cuales la función está definida y producirá un valor finito y real en la variable dependiente (Df= R). En otras palabras, el dominio de una función es el conjunto de valores de entrada permitidos para que la función de vuelva un valor real. El dominio de una función Df= R se representa como Df= R.

¿Cómo calcular el dominio de una función?

Para obtener el dominio de una función se deben determinar los valores reales para los que la función está bien definida. Esto se hace analizando la función (las posibles discontinuidades) y cómo se ha definido esta. Por ejemplo, para una función a trozos puede que se defina la función Df= R pero solo en el intervalo Df= R, por lo que, aunque la función Df= R está definida en todos los reales, el dominio será solamente Df= R. Es importante tener en cuenta que, en algunos casos, el dominio de una función puede ser implícito y no especificado explícitamente. En estos casos, es importante comprender el contexto y la naturaleza de la función para determinar su dominio, analizando qué valores son posibles y cuáles no.

Por ejemplo, si se analiza el tiempo que tarda una pelota en caer de una cierta altura, la función será polinómica y su dominio será, en principio, todos los números reales. Aun así, por el contexto del problema sabemos que el tiempo debe ser mayor o igual que 0, pues no tiene sentido pensar en que la pelota tarda un tiempo negativo en caer.

¿Cómo es el dominio de una función?

Si la función es algebraica, el dominio será todos los números reales, mientras que para muchas otras funciones el dominio será un intervalo, que puede ser tanto abierto (entre paréntesis) o cerrado (entre corchetes). El dominio de una función puede ser tanto disconexo, si está formado por varios intervalos serados (disjuntos); como conexo, si es un único intervalo o todos los números reales Df= R.

¿Por qué es importante el dominio de una función?

En primer lugar, el dominio de una función determina los valores permitidos de entrada para la función, por lo que, si intentamos evaluar la función para un valor que no está en el dominio, la función no estará definida y no tendrá un resultado válido. En segundo lugar, el dominio de una función puede influir en su comportamiento y propiedades, siendo muy distinta en su dominio y fuera de él. Por ejemplo, una función puede ser continua en su dominio, lo que significa que no tiene saltos ni discontinuidades.

¿Cómo depende una gráfica del dominio de la función representada?

El dominio de una función puede influir en su representación gráfica de muchas formas: si el dominio de una función es acotado (es decir, que no son todos los reales) será evidente en su gráfica, ya que no se extenderá a través de todo el plano. Por el contrario, si el dominio de una función es el conjunto de todos los números reales, su gráfica se extenderá a través de todo el plano. Además, si el dominio de una función no incluye ciertos puntos estos no podrán representarse en la gráfica o presentarán discontinuidades.

¿Cuál es el dominio de una función polinómica?

El dominio de una función polinómica es el conjunto de todos los números reales (Df= R), ya que cualquier número real puede ser utilizado como variable independiente para la función y producir un valor válido. 

¿Cuál es el dominio de una función lineal? ¿Y de una función cuadrática?

Las funciones lineales, al igual que las cuadráticas, son funciones polinómicas, luego su dominio será todos los números reales ().

¿Cuál es el dominio de una función racional?

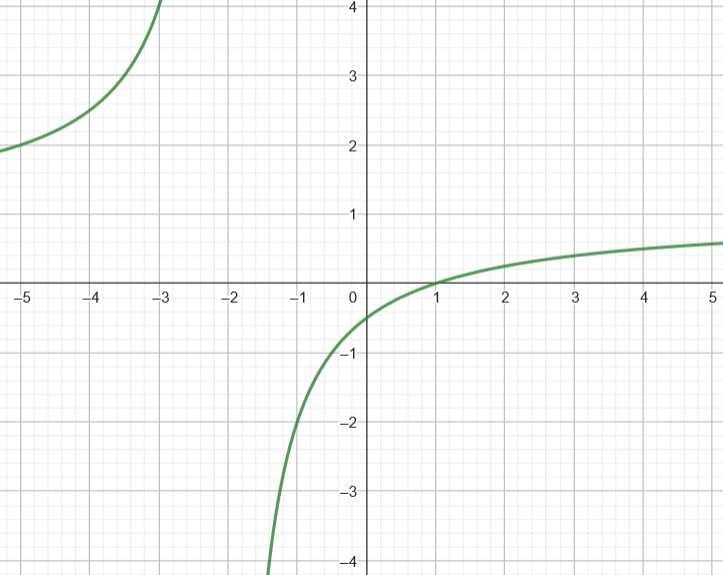
El dominio de una función racional es el conjunto de todos los números reales, excepto aquellos para los que el denominador de la función sea igual a cero. Esto se debe a que dividir por cero resultaría en una indeterminación del valor de la función (su valor sería “infinito”). 

Así, si una función racional tiene una expresión de la forma:

   y   

son funciones polinómicas, su dominio será el conjunto de todos los números reales, excepto aquellos que hacen

Si las funciones no son polinómicas, habrá que tener en cuenta el dominio de las distintas funciones también. 

Veámoslo con un ejemplo. Si se tiene la función,

  ,

donde tanto numerador como denominador son polinomios, entonces solo hace falta resolver la ecuación:

Finalmente, el dominio de la función será: , o, equivalentemente con intervalos: .

¿Cuál es el dominio de una función radical?

El dominio de una función radical , siendo √-1 el índice de la función y √-1 la variable independiente, es el conjunto de todos los valores reales para los cuales la función es un número real y no una cantidad compleja. Por ende, se deben dividir las funciones radicales en dos tipos para analizarse propiamente:

Funciones radicales de índice par: incluyendo aquí a la raíz cuadrada, este tipo de funciones son las funciones radicales con √-1 par. En este caso, no estará bien definida la raíz de número real negativo, pues al elevar un número cualquiera a una potencia par, siempre da un número positivo. Así, en el contexto de los números reales se dirá que √-1 no está bien definida. El dominio de una función radical de índice par serán entonces los números reales positivos y el 0.

Funciones radicales de índice impar: este tipo de funciones son las funciones radicales con √-1 impar. En este caso, como al elevar un número negativo a una potencia impar sí se puede obtener otro número negativo, la función puede definirse también para los valores reales negativos (por ejemplo, √-1. Así, su dominio son todos los números reales (Df= R). 

Supongamos ahora que el argumento de una función radical es otra función, es decir, Df= R con Df= R el índice y Df= R una función cualquiera. Entonces, se deberá tener cuenta también el dominio de la función argumento para determinar el dominio de la función radical, analizando las restricciones del argumento y expresando las restricciones como un sistema de ecuaciones que debe cumplirse. 

Por ejemplo: Df= R

Para esta función, como el argumento es una función polinómica no representa restricciones adicionales, por lo que se deberá cumplir que:

El dominio de la función será entonces Df= R.

¿Cuál es el dominio de una función exponencial?

El dominio de una función exponencial de la forma Df= R, donde Df= R es una constante positiva y Df= R es la variable independiente real, es el conjunto de todos los números reales (Df= R). En otras palabras, no hay restricciones en los valores de x para los cuales la función exponencial no está definida.

¿Cuál es el domino de una función logarítmica?

El dominio de una función logarítmica de la forma , donde f(x)=loge (x³+8)  es una constante positiva y Df= R

f(x)=loge (x³+8)

es la variable independiente real, está definido para valores de f(x)=loge (x³+8) mayores que cero (f(x)=loge (x³+8)). En otras palabras, el dominio de la función logarítmica es el conjunto de todos los números reales mayores que cero.

Esto se debe a que la función logarítmica es la inversa de una función exponencial, y las funciones exponenciales solo pueden devolver valores estrictamente positivos. Como la función exponencial es un número positivo elevado a otro, siempre será un valor positivo distinto de 0, pues:

f(x)=loge (x³+8)

Cabe destacar que para una función logarítmica habrá que tener en cuenta también la posible función que puede haber en el argumento. Esto es, si se tiene f(x)=loge (x³+8) con f(x)=loge (x³+8) una función cualquiera, entonces el dominio vendrá dado por el conjunto:

f(x)=loge (x³+8), además de las posibles restricciones que pueda tener f(x)=loge (x³+8) por sí misma.

Por ejemplo, considerando f(x)=loge (x³+8), en realidad se tiene el logaritmo neperiano, que es un logaritmo con base el número f(x)=loge (x³+8). Así, se está considerando la función:

f(x)=loge (x³+8)

Como la función Df= R no presenta restricciones, el dominio se podrá obtener únicamente con la restricción:

Df= R

El dominio de este ejemplo es entonces: Df= R.

¿Cuál es el dominio de una función trigonométrica?

El dominio de una función trigonométrica depende del tipo de función trigonométrica en cuestión. Para las tres funciones trigonométricas más importantes se tiene que:

• El dominio de la función seno, Df= R, es el conjunto de todos los números reales (Df= R). El dominio de la función coseno, Df= R, es el conjunto de todos los números reales
•  ().
• El dominio de la función tangente (tan(x)) es el conjunto de todos los números reales, excepto aquellos para los que la función coseno es nula. Esto es, el dominio está formado por los valores que cumplen que:

.

Es importante tener en cuenta que en una función tangente el argumento puede ser una función, es decir,

una función cualquiera. En este caso, será necesario tener en cuenta el dominio de la función argumento y se añadirán las restricciones internas de 

.

Ilustrándolo con un ejemplo, si se considera la función:

.

Después, la restricción de la función tangente será:

El dominio de la función será entonces:

Para seguir aprendiendo:

1- La inteligencia artificial ya esta aquí y se llama chat GPT

2- ¿Quieres ser una gran científica? Estamos a tu lado

3- Llévate el éxito

4- Recorrido de una función

5- Puntos de corte con los ejes