Por Resueltoos.com • 08-08-2023 • Matematicas
La combinatoria es una rama de las matemáticas que se ocupa del estudio de las diferentes formas de combinar, organizar o seleccionar elementos de un conjunto finito, sujeto a ciertas reglas y restricciones. Así, se centra en contar y enumerar (mediante números naturales) objetos de manera sistemática. La combinatoria abarca una amplia variedad de problemas y técnicas, incluyendo diagramas de árbol, principio de inclusión-exclusión o teoría de conjuntos. Algunos ejemplos comunes de problemas combinatorios incluyen:
Contar el número de formas en que se pueden organizar los elementos de un conjunto.
Determinar el número de subconjuntos que se pueden formar a partir de un conjunto dado.
Encontrar el número de caminos o rutas posibles en un grafo o en un tablero de ajedrez.
La combinatoria ha sido estudiada y desarrollada a lo largo de muchos siglos por diversos matemáticos, entre los que destacan:
Blaise Pascal (1623-1662): matemático, físico y filósofo francés que contribuyó a la combinatoria con, entre otros, el triángulo de Pascal, que muestra las combinaciones y coeficientes binomiales.
Pierre-Simon Laplace (1749-1827): matemático y astrónomo francés que realizó importantes contribuciones al campo de la probabilidad, sentando las bases para el estudio sistemático de las permutaciones y combinaciones.
Georg Cantor (1845-1918): matemático alemán conocido por su trabajo en la teoría de conjuntos y por desarrollar el concepto de cardinalidad de los conjuntos, incluyendo el estudio de los conjuntos infinitos y la enumeración de los números racionales.
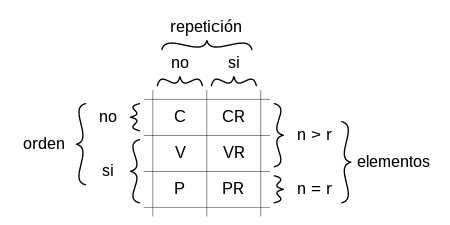
Hay tres características que determinan el tipo de combinatoria con el que se está trabajando: la influencia del orden, el número de elementos y las repeticiones.
Influencia del orden: Esta característica determina si el orden de los elementos seleccionados es relevante o no. Si el orden importa, se está tratando con permutaciones o variaciones, mientras que, si no importa, son combinaciones.
Relación entre el número de elementos disponibles (n) y los elementos presentes en cada suceso (r): Esta característica ayuda a distinguir entre las permutaciones y las variaciones, siendo que para las primeras se deben considerar todos los elementos disponibles en cada suceso (n=r) y para las segundas no (n>r).
Repeticiones en el suceso: Esta característica se refiere a si se permiten repeticiones al seleccionar elementos, habiendo una variante de cada tipo (permutaciones, variaciones y combinaciones) que permite la repetición y otra variante que no.
Basándonos en las tres características mencionadas anteriormente, existen seis tipos de combinatoria:
Permutaciones sin repetición: En este caso, se considera el orden de los elementos y todos los elementos disponibles intervienen en el suceso (n=r) y no se permiten repeticiones. El número de permutaciones sin repetición de n elementos es: P = n!, donde “!” significa factorial. Un ejemplo sería la cantidad de números de tres cifras distintas que pueden escribirse con el 3, el 5 y el 8: P = 3! = 3·2·1 = 6
Permutaciones con repetición: En este caso, se considera el orden de los elementos y todos los elementos disponibles intervienen en el suceso (n=r) y sí se permiten repeticiones. El número de permutaciones con repetición de n elementos entre los que algunos se repiten (uno se repite a veces, otro b veces, otro c veces...) es: PR = n!/(a!·b!·c·…).
Un ejemplo sería la cantidad de números de cinco cifras distintas que pueden escribirse con dos treses y dos cincos y un 8: PR = 5!/(2!·2!·1!) = 30
Combinaciones sin repetición: En este caso, no se considera el orden de los elementos y no se permiten repeticiones. Cada elemento se selecciona solo una vez. El número de elementos disponibles en el conjunto (n) debe ser mayor que el número de elementos en cada suceso (r). Así, el número de combinaciones sin repetición de n elementos tomados de r en r es: C = n!/(r!·(n-r)!)
Un ejemplo puede ser el número de equipos posibles de 2 personas que se pueden formar con 10 jugadores: C = 10!/(2!·8!) = 45
Combinaciones con repetición: Son análogas a las combinaciones sin repetición, pero ahora sí se permiten repeticiones.
Variaciones sin repetición: En este caso, sí se considera el orden de los elementos y no se permiten repeticiones. El número de elementos disponibles en el conjunto (n) debe ser mayor que el número de elementos en cada suceso (r). Así, el número de variaciones sin repetición de n elementos tomados de r en r es: V = n!/(n-r)!
Un ejemplo puede ser el número de formas de repartir un coche y una casa entre 6 personas, sabiendo que cada uno puede obtener solo una de las dos cosas: V = 6!/(6-2)! = 30
Variaciones con repetición: Aquí, se considera el orden de los elementos y se permiten repeticiones. El número de variaciones con repetición de n elementos tomados de r en r es: VR = n^r
Un ejemplo puede ser el número de formas de repartir un coche y una casa entre 6 personas, sin límite de premios por persona: VR = 2^6 = 64
El triángulo de Pascal es una representación visual de los coeficientes binomiales, que son números que aparecen en la combinatoria. Los coeficientes binomiales se utilizan para contar el número de formas en que se pueden seleccionar y organizar elementos de un conjunto, y el triángulo de Pascal muestra los coeficientes binomiales de manera estructurada, donde cada número en el triángulo es la suma de los dos números superiores.
La constante de Kaprekar es un número especial que se obtiene al seguir un procedimiento matemático específico sobre un número de varias cifras. La constante de Kaprekar se relaciona con la combinatoria a través de la idea de permutaciones, pues al realizar las operaciones necesarias para obtener la constante, se generan permutaciones de las cifras del número original. La combinatoria se utiliza para contar y enumerar todas las posibles permutaciones generadas en este proceso.
La combinatoria y la teoría de grafos están estrechamente relacionadas, ya que la combinatoria proporciona herramientas y técnicas para analizar y resolver problemas relacionados con grafos. La teoría de grafos estudia las propiedades y las relaciones entre los objetos llamados "grafos", que son estructuras compuestas por nodos (vértices) y conexiones entre ellos (aristas). Los conceptos combinatorios, como las permutaciones y las combinaciones, se utilizan en la teoría de grafos para contar el número de caminos posibles entre nodos, determinar la existencia de ciclos, analizar la coloración de grafos y resolver otros problemas relacionados con la estructura y la enumeración de grafos.
El binomio de Newton es una fórmula que permite expandir una expresión algebraica binomio elevado a una potencia. Esta fórmula tiene una estrecha relación con la combinatoria a través de los coeficientes binomiales, pues en la expresión del binomio aparece el coeficiente binomial C(n,k), que se calcula mediante la fórmula combinatoria: C(n, k) = n!/(k!·(n - k)!)
Donde "n" es el exponente del binomio, "k" es el índice del término en la expansión y "!" representa el factorial de un número.
La fórmula combinatoria se utiliza para contar el número de formas en que se pueden seleccionar y organizar "k" elementos de un conjunto de "n" elementos, que es exactamente lo que representa en el binomio de Newton, siendo clave en la descripción de identidades notables más complejas.
La combinatoria tiene aplicaciones prácticas en diversos campos, como la informática, la estadística, la teoría de juegos, la ingeniería, la biología, la física y muchos otros. Su estudio proporciona herramientas y métodos para resolver problemas relacionados con la optimización de recursos, el análisis de algoritmos, la planificación, la codificación y otros aspectos importantes en ciencias y tecnología, siendo algunas de sus principales utilidades:
Conteo y enumeración: La combinatoria proporciona herramientas y técnicas para contar y enumerar objetos y estructuras de manera sistemática. Esto es útil en situaciones donde es necesario determinar el número de posibilidades o configuraciones, como en la planificación de eventos, el análisis de algoritmos, el diseño de experimentos y otros contextos donde es esencial conocer la cantidad exacta de combinaciones o permutaciones.
Probabilidad y estadística: La combinatoria es fundamental en el estudio de estos campos, utilizándose para calcular probabilidades, resolver problemas de conteo en experimentos aleatorios, analizar la distribución de probabilidad, estimar muestras y realizar cálculos de combinatoria en problemas estadísticos complejos.
Diseño y optimización: La combinatoria se utiliza en el diseño de estructuras y sistemas eficientes. En el diseño combinatorio, se emplean principios y técnicas combinatorias para construir sistemas de diseño con propiedades específicas, como los diseños de bloques, los planos proyectivos y las matrices de Hadamard.
Criptografía y seguridad: La combinatoria tiene aplicaciones en la criptografía, donde se utilizan técnicas de conteo y combinaciones para el diseño de algoritmos criptográficos seguros. Los principios combinatorios se emplean en la generación de claves, la construcción de códigos y la seguridad de sistemas de comunicación.
Teoría de juegos: La combinatoria se aplica en la teoría de juegos, donde se estudian los comportamientos estratégicos y las decisiones en situaciones de interacción entre jugadores. Los conceptos combinatorios se utilizan en el análisis de combinaciones estratégicas, la determinación de equilibrios de Nash y la resolución de juegos complejos.
Por ultimo no queremos despedirnos sin animaros a examinar nuestro sistema de aprendizaje en matemáticas, Resueltoos. A través de su interacción interactiva, enfoque paso a paso y recursos cuidadosamente diseñados, Resueltoos ha pavimentado el camino para una comprensión profunda y duradera de conceptos complejos. Al caminar junto a Resueltoos, los alumnos no solo dominan las técnicas de combinatoria, sino que también cultivan un amor genuino por las matemáticas. Esta plataforma no solo es un lugar para resolver problemas, sino un espacio donde las mentes curiosas florecen y se expanden, abrazando la belleza intrínseca de la lógica matemática.
Ya sea que un estudiante se encuentre al inicio de su viaje matemático o busque perfeccionar su comprensión en combinatoria, Resueltoos ofrece una experiencia educativa única y valiosa. Su éxito para enseñar matemáticas es innegable, forjando una generación de mentes afiladas y apasionadas por la resolución de problemas. En última instancia, Resueltoos no solo enseña matemáticas, sino que nutre el crecimiento intelectual y despierta la fascinación por el infinito mundo de los números. Así que, no busques más, tu camino hacia la excelencia matemática comienza aquí, con Resueltoos. ¡Explora, aprende y déjate maravillar!
1- La inteligencia artificial chat GPT
2- ¿Quieres ser una gran científica?
5- Puntos de corte con los ejes
Dominio de una función
01-06-2023
Recorrido de una función
02-03-2023
Puntos de corte con los ejes
05-05-2023
Puntos de corte de funciones racionales, logarítmicas, trigonométricas
02-03-2023
