Por Resueltoos.com • 30-09-2023 • Matematicas
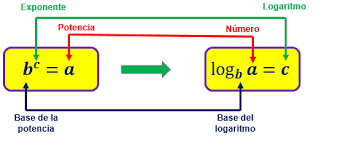
Un logaritmo es una función matemática que representa el exponente al que debe elevarse una base dada para obtener un cierto valor. Formalmente, si se tiene una base “b” y un valor “x”, el logaritmo de “x” en base “b” se representa como log_b (x), donde “x” es el argumento del logaritmo y “b” es la base. De esta forma, un logaritmo se define como el exponente al que debe elevarse “b” para obtener “x”: b^(log_b (x)) = x
Por ejemplo, si b=2 y x=8, entonces log₂(8)=3 porque 2^3=8.
El desarrollo de los logaritmos se intensificó significativamente entre los siglos XVI y XVII debido a la necesidad de simplificar ciertos cálculos matemáticos. En 1614, John Napier presentó públicamente el método de los logaritmos en su obra titulada Mirifici Logarithmorum Canonis Descriptio (Descripción de la asombrosa regla de los logaritmos). Napier observó que las operaciones de multiplicación o división entre las potencias se correspondían con operaciones de suma o resta de los exponentes de dichas potencias. De este razonamiento surgió la idea de reemplazar cada operación de multiplicación por una operación de suma: a^n*a^m = a^(n+m)
Sin embargo, Napier se encontró con un problema: si utilizaba una secuencia de potencias enteras de una base entera, como por ejemplo el número dos, esto no resultaba práctico para el cálculo debido a las grandes diferencias entre los términos sucesivos de la secuencia. La idea central en el trabajo de Napier se resume de la siguiente manera: con el fin de lograr que los términos de una serie geométrica compuesta por las potencias enteras de un número específico estén cercanos entre sí, es necesario seleccionar un número que esté muy próximo a uno. Napier optó por elegir el número 1-10^(-7) = 0,9999999. Entonces, los términos de la progresión (decreciente) de potencias enteras crecientes, están muy próximos entre sí.
Para evitar el uso de decimales, multiplicó todas las potencias por 10^7. De esta forma: N = 10^7*(1-10^(-7))^L
Donde L es el logaritmo de Napier del número N.
Las reglas de logaritmos propuestas por Napier difieren de las que utilizamos en la actualidad. Son más complicadas, ya que en su sistema se establecía que el logaritmo de 1 era distinto de 0 (se acordaba que log 10^8 =1). Por ejemplo, en el caso de los logaritmos de productos o cocientes, no se podía afirmar que fueran equivalentes a la suma o la diferencia de los logaritmos respectivos. En la misma época que Napier, surgió de forma independiente el suizo Joost Burgi quién creó un método para calcular logaritmos y construyó una tabla con aproximadamente 20,000 términos. Sin embargo, fue el matemático inglés Henry Briggs quien los adaptó para valores más fáciles de utilizar mediante logaritmos decimales, como los que conocemos hoy.
Los logaritmos tienen varias propiedades fundamentales que los hacen útiles para una gran variedad de aplicaciones. Algunas de ellas son:
Suma de logaritmos: La suma de dos logaritmos con base común “b” y argumentos “x” e “y” respectivamente, es igual al logaritmo de base “b” y argumento “x*y”: log_b(x) + log_b(y) = log_b(x*y)
Resta de logaritmos: La resta de dos logaritmos con base común “b” y argumentos “x” e “y” respectivamente, es igual al logaritmo de base “b” y argumento “x/y”: log_b(x) - log_b(y) = log_b(x/y)
Logaritmo de una potencia: El logaritmo de una potencia es igual al exponente de la potencia multiplicado por el logaritmo de la base de la potencia inicial: log_b(x^a) = a*log_b(x)
Logaritmo de la base: Un logaritmo con el mismo valor para la base y el argumento es igual a la unidad: log_b(b) = 1
Logaritmo de una raíz: Un logaritmo con argumento de la forma ᵐ √x^n y base “b”, es igual al logaritmo de “x” multiplicado por “m/n”, esto es: log_b (ᵐ√x^n) = (m/n)*log_b(x)
Logaritmo de la unidad: Un logaritmo con argumento la unidad siempre da como resultado 0, independientemente de la base escogida.
El logaritmo neperiano, también conocido como logaritmo natural, se refiere al logaritmo en base al número "e", que es una constante matemática aproximadamente igual a 2.71828. El logaritmo neperiano se representa comúnmente como "ln" o simplemente como "log", sin indicar una base específica, lo que implica que se está utilizando la base "e", esto es: ln (x) = log_e (x). La importancia del logaritmo neperiano radica en varias áreas de las matemáticas y las ciencias, donde desempeña un papel fundamental:
Cálculo y análisis matemático: El logaritmo natural es esencial en cálculo diferencial e integral. La derivada de ln(x) es 1/x, lo que lo convierte en una función importante en la resolución de problemas de optimización, tasas de cambio y otros conceptos fundamentales en cálculo.
Probabilidad y estadísticas: En estadísticas, el logaritmo natural se utiliza para transformar datos que siguen una distribución logarítmica en base 10 a datos que siguen una distribución normal, lo cual es, en muchas ocasiones, de gran ayuda para estudiar tendencias y relacionar magnitudes.
Física: En física, el logaritmo natural aparece en la descripción de fenómenos como la difusión de partículas, la ley de enfriamiento de Newton y la ley de los gases ideales.
Los logaritmos decimales o en base 10 se utilizan en diversas disciplinas científicas y técnicas para representar y comparar magnitudes que abarcan rangos muy amplios. Algunas de las magnitudes que se miden comúnmente en una escala logarítmica decimal incluyen:
Magnitud de terremotos: La escala de Richter mide la magnitud de los terremotos en una escala logarítmica decimal. Un aumento de un punto en la escala de Richter representa un aumento de diez veces en la amplitud de las ondas sísmicas y aproximadamente 31.6 veces más energía liberada.
Niveles de sonido: La escala de decibelios (dB) se utiliza para medir niveles de sonido. La relación entre la intensidad del sonido y los decibelios es logarítmica, y un incremento de 10 dB representa un aumento de diez veces en la intensidad del sonido percibido.
Acidez y alcalinidad (pH): La escala de pH es logarítmica, y cada unidad de cambio en el pH representa un cambio de diez veces en la concentración de iones hidronio (H3O+) en una solución.
Magnitudes astronómicas: En astronomía, se utilizan escalas logarítmicas para describir magnitudes de estrellas y objetos celestes. La magnitud aparente de una estrella es una escala logarítmica inversa, donde las estrellas más brillantes tienen magnitudes negativas y las menos brillantes tienen magnitudes positivas.
Además de su uso para diferentes magnitudes, los logaritmos decimales son de gran utilidad en matemáticas, física y estadística para la simplificación de cálculos aritméticos, resolución de ecuaciones exponenciales y el análisis de datos y estadísticas.
Para calcular el logaritmo de un número complejo “z”, se utiliza la fórmula del logaritmo complejo: log (z) = ln |z| + iθ
Donde “ln” es el logaritmo natural, “|z|” representa el módulo del número complejo “z” y “θ” es el argumento de “z”, esto es, el ángulo que el vector que conecta el origen con “z” forma con el eje positivo de las abscisas en el plano complejo. Así, tomando por ejemplo el número imaginario z = 3 + 4i, donde “i” es la unidad imaginaria, para calcular el logaritmo de “z” se procederá de la siguiente forma:
Primero se calcula el módulo de “z”: |z| = √(3²+4²) = √(9+16) = √25 = 5
A continuación, se calcula el argumento de “z”, para lo que puedes usar la función arco tangente de la razón entre la parte imaginaria y la parte real de “z”. En este caso: θ = arctan(4/3) ≈ 0,93 radianes.
Finalmente, se aplica la expresión para el logaritmo complejo: log(z) = ln|z| + iθ = ln(5) + i * 0.93 radianes.
En el conjunto de números reales, el logaritmo de un número negativo o igual a cero no está definido, ya que no existe un número real “x” tal que 10^x sea igual a un número negativo o igual a cero. Esto se debe a que las potencias de 10 (o cualquier base positiva) siempre son números positivos.
En el conjunto de números complejos, por el contrario, es posible definir logaritmos de números negativos introduciendo el logaritmo complejo. Esto se debe a que, al calcular el módulo de “z” (que corresponderá a la parte real de la solución), siempre va a dar como resultado un valor positivo, eliminando los problemas para los logaritmos reales negativos. Además, si el logaritmo a tratar es un logaritmo natural, el cálculo se simplifica notablemente, pues se puede hacer uso de la identidad de Euler: e^(iπ) + 1 = 0
Despejando la exponencial y tomando logaritmos naturales a ambos lados se obtiene: ln(iπ) = ln(-1)
definiendo así el valor del logaritmo para -1. De esta forma, podemos calcular el valor de cualquier logaritmo negativo aplicando las propiedades de los logaritmos: ln(-a) = ln(a) + ln(-1) = ln(a) + iπ
Sumérgete en Resueltoos, la plataforma educativa que está revolucionando la enseñanza de las matemáticas. Ofrecemos ventajas invaluables para padres y alumnos por igual. Los padres confían en nuestros tutores virtuales expertos y en el seguimiento personalizado para garantizar el éxito académico de sus hijos. Los alumnos adoran Resueltoos gracias a su enfoque divertido y dinámico con juegos interactivos, permitiéndoles aprender en cualquier momento y lugar. Transformamos las matemáticas de una tarea difícil en una destreza que abre puertas hacia un futuro prometedor. ¡Suscríbete ahora y prepárate para un emocionante viaje educativo!
1- La inteligencia artificial chat GPT
2- ¿Quieres ser una gran científica?
5- Puntos de corte con los ejes
Dominio de una función
01-06-2023
Recorrido de una función
02-03-2023
Puntos de corte con los ejes
05-05-2023
Puntos de corte de funciones racionales, logarítmicas, trigonométricas
02-03-2023
