Una matriz es una estructura matemática bidimensional compuesta por filas y columnas de elementos, dispuestos en forma rectangular. Estos elementos pueden ser números, símbolos o expresiones algebraicas. La matriz se denota con letras mayúsculas, por ejemplo, A, B o C y la disposición de sus elementos se representa de la siguiente manera:

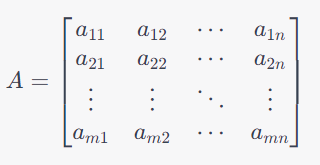
Donde a_(ij) hace referencian al elemento en la fila i y columna j de la matriz. El tamaño de una matriz se describe por el número de filas (m) y el número de columnas (n). Por ejemplo, una matriz de tamaño “m×n” tiene “m” filas y “n” columnas.

¿Cuál es el origen de las matrices y las ecuaciones matriciales?

Las raíces históricas de las matrices se remontan a épocas antiguas. Se puede encontrar evidencia de matrices en la literatura china, específicamente en el registro de un cuadrado mágico de 3 por 3 que data del año 650 a.C.  La historia del uso de matrices para resolver ecuaciones lineales es extensa y diversa. Un texto matemático chino conocido como “Nueve capítulos sobre el Arte de las matemáticas”, escrito entre los años 300 a.C. y 200 a.C., es el primer ejemplo conocido de la aplicación de matrices para la resolución de sistemas de ecuaciones simultáneas. En el capítulo séptimo de este antiguo texto se introduce por primera vez el concepto de determinante, dos mil años antes de que matemáticos como Seki Kowa y Gottfried Leibniz lo publicaran de manera independiente. 

Los primeros “cuadrados mágicos” de orden 5 y 6 se registraron en Bagdad en el año 983, específicamente en la “Enciclopedia de la Hermandad de Pureza”. El término “matriz” como tal fue acuñado en 1848 por J. J. Sylvester. En 1853, Hamilton realizó contribuciones significativas a la teoría de matrices, y en 1858, Cayley introdujo la notación matricial como una forma abreviada de escribir un sistema de “m” ecuaciones lineales con “n” incógnitas. Matemáticos notables como Grassmann, Fröbenius y Neumann también hicieron importantes aportes a la teoría de matrices a lo largo de la historia.

¿Qué es la matriz identidad?

La matriz identidad, denotada como I_n o simplemente I, es una matriz cuadrada n×n que tiene unos en la diagonal principal y ceros en el resto de sus elementos. La propiedad fundamental de la matriz identidad es que, cuando se multiplica por cualquier otra matriz, no modifica a dicha matriz, es decir, I*A=A*I=A para cualquier matriz A del tamaño adecuado.

¿Cómo sumar y restar matrices?

La suma y resta de matrices se realiza elemento por elemento. Dos matrices deben tener el mismo tamaño para que estas operaciones sean posibles. Si A y B son matrices del mismo tamaño, entonces la suma A+B y la resta A−B se definen como sigue:

¿Cómo multiplicar matrices?

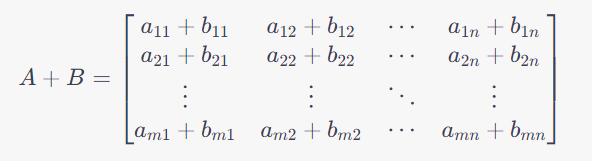
El producto de matrices es una operación más compleja. Para multiplicar dos matrices A y B, el número de columnas en A debe ser igual al número de filas en B. Si A es una matriz de tamaño m×n y B es una matriz de tamaño n×p, entonces su producto, denotado como AB, será una matriz de tamaño m×p cuyos elementos se calculan de la siguiente forma: c_(ij) = a_(i1)*b_(1j) + a_(i2)*b_(2j) + … + a_(in)*b_(nj)

La multiplicación de matrices es asociativa y distributiva, pero no conmutativa, es decir, en general, A*B≠B*A, lo que subraya la importancia de mantener el orden de la multiplicación. Existen ciertos casos en los que la multiplicación de matrices es conmutativa, por ejemplo:

Si una de las matrices es la matriz identidad.

Si ambas matrices son cuadradas y diagonales.

Si la matriz A es la inversa de B o viceversa, la multiplicación de ambas da como resultado la matriz identidad, sin importar el orden de la multiplicación.

En el caso del producto de una matriz por un escalar, la multiplicación también es conmutativa y se lleva a cabo multiplicando cada elemento de matriz por el escalar. 

¿Cómo calcular la potencia de una matriz?

Para calcular la potencia “n” de una matriz A, se debe tener en cuenta, en primer lugar, que la matriz sea cuadrada. Si la potencia “n” es un número bajo, como 2 o 3, se multiplicará la matriz por sí misma tantas veces como indique la potencia.  Sin embargo, este método puede llegar a ser bastante tedioso para potencias elevadas. En estos casos se buscará un patrón, es decir, se prueba a calcular A², A³, A⁴ y se observa si los elementos de matriz se repiten o si siguen alguna sucesión lógica.

Este procedimiento no es siempre válido, pues algunas matrices no seguirán ningún tipo de patrón que permita calcular la potencia n-ésima. Otra forma de obtener la potencia n-ésima de A es diagonalizar la matriz (sólo si es posible), esto es, expresarla como A=P*D*P¯¹, donde P es una matriz de autovectores y D es una matriz diagonal que contiene los autovalores de A. Entonces el cálculo de la potencia se simplifica notablemente: Aⁿ=P*Dⁿ*(ⁿⁿ)¯¹

Donde Dⁿ es la matriz diagonal con los autovalores de A elevados a la potencia “n” en su diagonal principal.

¿Qué es una matriz transpuesta?

La matriz transpuesta de una matriz A, denotada como A^T, se obtiene intercambiando sus filas por sus columnas. Así, si A es una matriz m×n, entonces A^T será una matriz n×m. 

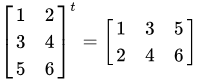
La transpuesta de una matriz es importante en aplicaciones como la resolución de sistemas de ecuaciones lineales y en la multiplicación de matrices.

¿Cómo calcular la inversa de una matriz?

Para calcular la matriz inversa de una matriz A, se deben seguir los siguientes pasos:

Verificar que A sea invertible: Una matriz es invertible (o tiene una matriz inversa) si su determinante (det(A)) no es igual a cero. Si el determinante de A es cero, la matriz no tiene inversa y no puedes continuar con el cálculo.

Encontrar la matriz adjunta de A: La matriz adjunta de A, denotada como adj(A) se calcula tomando la matriz de los cofactores de A y luego transponiéndola. Cada elemento de la matriz adjunta se calcula como el cofactor correspondiente al elemento de la matriz original. 

Calcular la matriz inversa de A: La matriz inversa de A, denotada como A¯¹, se obtiene al multiplicar la matriz adjunta de A por el inverso del determinante de A, esto es: A¯¹ = adj(A)^T/det(A)

Esta matriz es útil para resolver sistemas de ecuaciones lineales y realizar otras operaciones matriciales, debido a la propiedad fundamental: A¯¹*A=A*A¯¹=I. Donde I es la matriz identidad. Es importante mencionar que no todas las matrices tienen una matriz inversa, solo las matrices cuadradas cuyo determinante no es cero. Además, si una matriz tiene inversa, ésta es única. Por lo tanto, si se calcula la matriz inversa de una matriz invertible, se obtendrá siempre el mismo resultado, independientemente del método empleado para calcularla.

¿Qué es una ecuación matricial?

Las ecuaciones matriciales son aquellas que tienen como incógnita una matriz. Estas ecuaciones permiten representar relaciones entre matrices y vectores. Una ecuación matricial típica se expresa de la siguiente forma: A*X = B. Donde “A” es una matriz conocida, “X” es la matriz desconocida que se está intentando encontrar y “B” es otra matriz conocida.

Si la matriz A es invertible, entonces se puede encontrar la solución única X=A¯¹*B, donde A¯¹ es la matriz inversa de A. En caso de que A no sea invertible, el sistema puede tener múltiples soluciones o ser incompatible.

¿Cómo resolver ecuaciones matriciales?

Para resolver ecuaciones matriciales, en primer lugar, se despeja la matriz desconocida y, a continuación, se llevan a cabo las operaciones utilizando las matrices resultantes. Un ejemplo sencillo es el siguiente: AX – B = C

Donde A, B, C son matrices conocidas y X es la matriz que queremos encontrar. Todas las matrices que estén sumando/restando, pasarán al otro lado de la ecuación restando/sumando, respectivamente. En este ejemplo la ecuación quedaría: AX = C + B

Cuando aparezcan matrices multiplicando a la matriz incógnita, se multiplicará a ambos lados de la ecuación por la matriz inversa de la matriz que se quiere eliminar (en este ejemplo A), pues A^(-1)*A es igual a la matriz identidad. La ecuación queda entonces como: A = A¯¹*(C + B)

Es de vital importancia colocar la matriz inversa en la misma posición a ambos lados, esto es, si multiplico A¯¹*AX , entonces en el lado derecho de la ecuación se debe poner A¯¹*(C+B) pues, como bien se ha mencionado anteriormente, A*B ≠ B*A.

¿Qué es una matriz simétrica?

Una matriz simétrica es una matriz cuadrada que es igual a su propia transpuesta. En otras palabras, si tienes una matriz simétrica A, entonces se cumple que: A=A^T. Esto significa que los elementos de una matriz simétrica son simétricos con respecto a su diagonal principal.

¿Qué es una matriz diagonal?

Una matriz diagonal es una matriz cuadrada en la que todos los elementos fuera de la diagonal principal son cero. La diagonal principal es la serie de elementos que se extienden desde la esquina superior izquierda de la matriz (elemento a_1,1) hasta la esquina inferior derecha (elemento a_n,n).

Explora Resueltoos, la innovadora plataforma educativa que está cambiando la forma en que se aprenden las matemáticas. Brindamos ventajas excepcionales tanto para padres como para estudiantes. Para los padres, Resueltoos ofrece tutores virtuales altamente capacitados y seguimiento personalizado, lo que les proporciona tranquilidad sobre el progreso académico de sus hijos. A los estudiantes les encanta Resueltoos por su enfoque interactivo y divertido con juegos educativos que hacen que las matemáticas sean atractivas. Nuestra plataforma convierte las matemáticas en una habilidad esencial que allana el camino hacia un futuro exitoso. ¡Suscríbete ahora y prepárate para un viaje educativo excepcional!

Seguir aprendiendo:

1- La inteligencia artificial chat GPT

2- ¿Quieres ser una gran científica?

3- Llévate el éxito

4- Dominio de una función

5- Puntos de corte con los ejes