Consigue 5 días de prueba gratuita registrándote ahora
En nuestro e-book gratuito, encontrarás estrategias probadas que ayudarán a tu hijo a mejorar sus hábitos de estudio. ¡Transforma su manera de estudiar hoy mismo!

Resueltoos.com Física y química
28-12-2023
El movimiento parabólico es el desplazamiento efectuado por un objeto cuya trayectoria sigue la forma de una parábola. Este tipo de movimiento es el resultado de la combinación de un movimiento rectilíneo uniforme en la dirección horizontal y un movimiento rectilíneo uniformemente acelerado en la dirección perpendicular.
Algunos aspectos clave del movimiento parabólico incluyen:
Velocidad inicial (V₀): La velocidad con la que se lanza el objeto determina la forma y las dimensiones de la trayectoria parabólica.
Ángulo de lanzamiento (θ): El ángulo con respecto a la horizontal en el cual se lanza el objeto también afecta la forma de la trayectoria. El ángulo de lanzamiento óptimo para alcanzar la máxima distancia horizontal es de 45 grados, siempre y cuando no haya resistencia del aire u otros factores externos.
Alcance y altura máxima: El alcance se refiere a la distancia horizontal máxima alcanzada por el objeto, mientras que la altura máxima es la posición que tiene componente vertical máxima.
Gravedad: La aceleración debida a la gravedad es una constante que afecta la componente vertical del movimiento parabólico. En la Tierra, la gravedad actúa hacia abajo y contribuye a la aceleración vertical del objeto.
El movimiento parabólico se encuentra en muchas situaciones del mundo real, como el lanzamiento de proyectiles, el vuelo de objetos lanzados, la trayectoria de un objeto en un campo gravitatorio, entre otros.
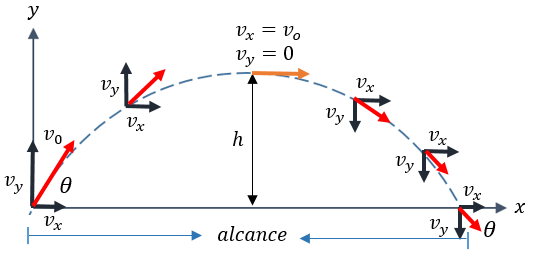
Para estudiar el movimiento parabólico, se deben separar las componentes vertical y horizontal de la velocidad inicial y aceleración, pues cada eje tiene un tipo de movimiento diferente. Así, se obtiene:
Descomposición de la velocidad inicial: Separamos la velocidad inicial en la componente horizontal y la componente vertical usando la relación trigonométrica del seno y coseno. De esta forma, la componente vertical de la velocidad inicial se define como: v₀y = v₀ * sin(θ)
Mientras que la componente horizontal de la velocidad inicial se define como: v₀x = v₀ * cos(θ)
Si inicialmente se conocen ambas componentes, pero no la velocidad inicial total, es posible calcularla mediante la raíz cuadrada que se muestra en la siguiente expresión: v₀ = sqrt(v₀_x² + v₀_y²)
Descomposición de la aceleración: La aceleración también se descompone en dos componentes: una en la dirección horizontal (a_x = 0) y otra en la dirección vertical (a_y = g). La aceleración horizontal es cero porque no hay fuerzas horizontales externas afectando al objeto, mientras que en el eje vertical el movimiento se ve afectado por la gravedad (g = -9,81 m/s^2).
No hay un único descubridor del movimiento parabólico, ya que los principios relacionados con este tipo de movimiento han sido comprendidos y desarrollados a lo largo del tiempo por varios científicos y matemáticos. Sin embargo, algunas contribuciones clave son:
Arquímedes: Aunque no abordó directamente el movimiento parabólico, Arquímedes realizó contribuciones significativas a la geometría y al estudio de las secciones cónicas, incluida la parábola. Su trabajo en el cálculo de áreas y volúmenes fue esencial para el desarrollo posterior de conceptos relacionados con el movimiento parabólico.
Galileo Galilei: Pionero de la ciencia moderna, realizó experimentos y observaciones detalladas sobre el movimiento de los objetos. Aunque no formuló las ecuaciones matemáticas exactas del movimiento parabólico, sus investigaciones sobre la caída de los cuerpos y la descripción del movimiento de proyectiles sentaron las bases para futuros desarrollos en este campo.
Johann Bernoulli: Este matemático suizo contribuyó al desarrollo de la teoría matemática del movimiento de proyectiles. A través de sus investigaciones, ayudó a establecer las ecuaciones del movimiento parabólico y a comprender mejor cómo la gravedad afecta a los objetos en movimiento.
Isaac Newton: Newton formuló las leyes del movimiento y la ley de la gravitación universal. Sus contribuciones fueron fundamentales para comprender el movimiento parabólico y sentaron las bases para el desarrollo de la mecánica clásica.
El movimiento parabólico es una combinación del MRUA y el MRU, de forma que, el movimiento en el eje horizontal sigue un MRU, ya que, en ausencia de fuerzas horizontales externas, no hay aceleración horizontal constante, mientras que el movimiento en el eje vertical sigue un MRUA, debido a la influencia de la gravedad, que hace variar la componente vertical de la velocidad. La interacción de estos dos componentes genera la forma de parábola en la trayectoria.
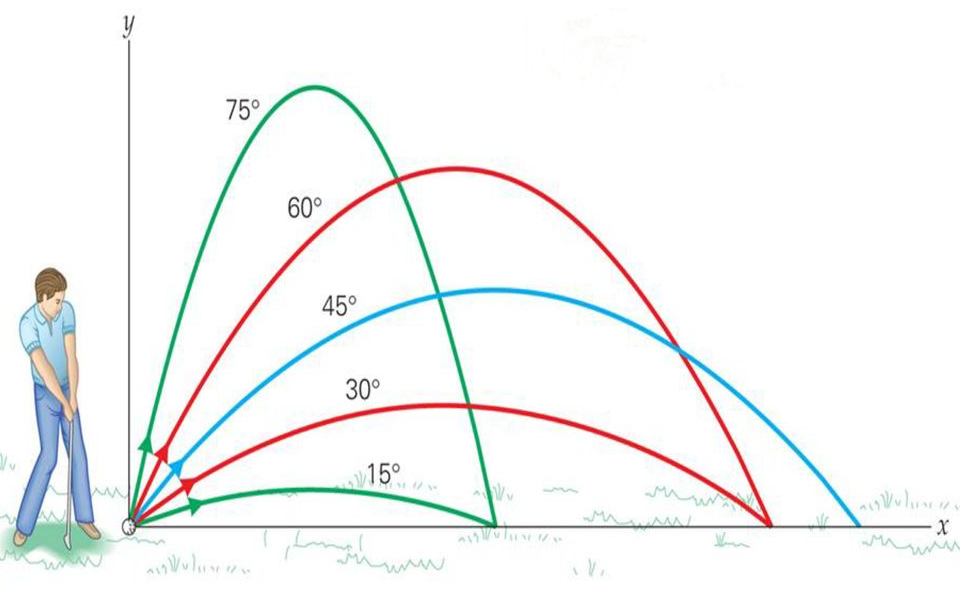
Tras hallar las componentes horizontal y vertical de la velocidad y la aceleración, es fácil dividir el movimiento en dos tipos de movimientos diferentes: MRU en el eje horizontal y MRUA en el eje vertical, como ya se ha dicho previamente. Las ecuaciones del movimiento serán entonces las propias de estos dos movimientos:
La velocidad es constante y es igual al valor de la componente horizontal de la velocidad inicial del movimiento parabólico.
Donde “v₀y” es la velocidad inicial del eje vertical del movimiento parabólico y “a_y” es igual a la gravedad. Estas ecuaciones se deben adaptar a las condiciones iniciales de cada problema, pudiendo variar la posición inicial del objeto, el ángulo de lanzamiento y la velocidad inicial del movimiento.
El ángulo de salida inicial (θ) en un movimiento parabólico se puede calcular considerando la relación entre las componentes horizontal y vertical de la velocidad inicial. Utilizando relaciones trigonométricas, es sencillo calcular las componentes horizontal y vertical de la velocidad inicial:
v₀x = v₀ * cos(θ)
v₀y = v₀ * sin(θ)
Si conocemos los valores de v₀x y v₀y, es posible hallar el ángulo de salida inicial despejando de cualquiera de las dos expresiones anteriores:
θ = arccos(v₀x / v₀)
θ = arcsin(v₀y / v₀)
En el caso de que la velocidad inicial total no sea conocida, es posible calcular el ángulo de salida inicial utilizando la tangente:
v₀y / v₀x = tan(θ)
Despejando para θ:
θ = arctan(v₀y / v₀x)
La altura y el alcance máximos de un movimiento parabólico se obtienen analizando las ecuaciones que describen el movimiento vertical y horizontal del movimiento parabólico.
La altura máxima (y_max) se alcanza cuando la velocidad vertical (vy) es igual a cero. Para encontrar el tiempo (t_max) en el cual esto ocurre, recurrimos a las ecuaciones empleadas en el eje vertical (MRUA):
v₀y + a_y * t_max = 0
Resolviendo para t_max:
t_max = -v₀y / a_y
A continuación, se sustituye este tiempo en la ecuación de posición vertical para obtener la altura máxima:
y_max = y₀ + v₀y * t_max + (a_y * t_max^2) / 2
Debemos destacar que, en la altura máxima, la velocidad horizontal es igual a la velocidad total. Por otra parte, el alcance máximo se obtiene cuando la posición vertical es cero, es decir, cuando el objeto toca el suelo. En este caso, es necesario primero trabajar en el eje vertical para hallar el tiempo de vuelo, para después pasar a las ecuaciones del eje horizontal para hallar el alcance máximo (x_max). Para encontrar el tiempo total de vuelo, recurrimos a ecuación de posición vertical estableciendo y = 0.
0 = y₀ + v₀y * t_vuelo + (a_y * t^2) / 2
Esta ecuación cuadrática tiene dos soluciones para el tiempo. Como es obvio, la solución negativa no es válida (pues el tiempo no puede ser negativo), siendo la solución correcta la positiva. Otra forma de calcular el tiempo total de vuelo es, una vez conocido el tiempo para llegar a la altura máxima, multiplicar este valor por dos. Esto se debe a que el movimiento parabólico es siempre simétrico, es decir, un objeto tardará el mismo tiempo en subir que en bajar, siempre y cuando no se altere el movimiento con fuerzas externas. Finalmente, se puede usar el tiempo total de vuelo para calcular el alcance máximo (x_max) utilizando la ecuación de posición horizontal:
x_max = x₀ + v₀x * t_vuelo

El movimiento parabólico tiene diversas aplicaciones en distintas áreas. Algunas de las más comunes son:
Lanzamiento de proyectiles: El lanzamiento de proyectiles, como balas, cohetes, o cualquier objeto arrojado al aire, sigue una trayectoria parabólica. Este concepto es fundamental en la balística y en el diseño de sistemas de lanzamiento.
Deportes: En deportes como el baloncesto, el fútbol, el golf o el béisbol, los movimientos de lanzamiento y pateo siguen trayectorias parabólicas. Comprender el movimiento parabólico es esencial para mejorar la precisión y la distancia en estos deportes.
Satélites y cohetes espaciales: En la ingeniería espacial, los lanzamientos de cohetes y la órbita de satélites pueden describirse mediante ecuaciones parabólicas. La comprensión del movimiento parabólico es crucial para el diseño de trayectorias y la planificación de misiones espaciales.
Simulaciones y videojuegos: En el desarrollo de simuladores y videojuegos, la representación realista del movimiento de objetos arrojados o disparados se logra mediante modelos basados en el movimiento parabólico.
Mediciones de distancia: En la topografía y la medición de distancias, se pueden utilizar métodos basados en el movimiento parabólico, como el método de telemetría, para determinar distancias entre objetos.
Te damos la bienvenida a Resueltoos, la plataforma educativa líder que está transformando la enseñanza de las matemáticas. Nuestra propuesta ofrece beneficios destacados tanto para padres como para estudiantes. Los padres confían en Resueltoos gracias a nuestros tutores virtuales altamente cualificados y el seguimiento personalizado, asegurando un sólido éxito académico para sus hijos. Los estudiantes encuentran en Resueltoos un enfoque interactivo y divertido, con juegos educativos que hacen que las matemáticas sean emocionantes. Cambiamos las matemáticas de un desafío a una habilidad esencial que allana el camino hacia un futuro brillante. ¡Inscríbete ahora y prepárate para una experiencia educativa excepcional!
1- La inteligencia artificial chat GPT
2- ¿Quieres ser una gran científica?
5- Puntos de corte con los ejes
Resueltoos
02-06-2023

Resueltoos.com
El movimiento circular se refiere a cualquier movimiento en el cual un objeto se mueve alrededor de un punto central en una trayectoria circular
Resueltoos
01-06-2023
Resueltoos.com
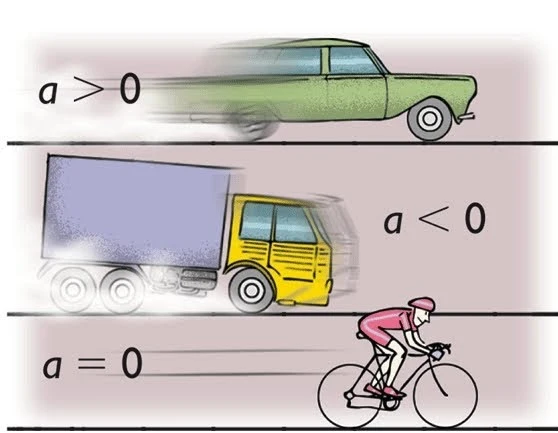
Un movimiento rectilineo es aquel en el que un objeto se mueve en linea recta, es decir, su trayectoria no presenta curvas ni cambios de direccion
Resueltoos
02-06-2023
Resueltoos.com
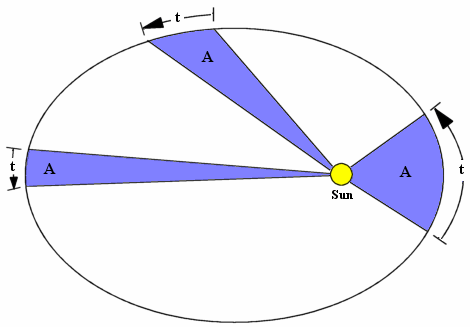
Las leyes de Kepler son tres principios empíricos que describen el movimiento de los planetas alrededor del Sol
Descubre nuestro e-book repleto de secretos para aprobar cada examen
