Estudio de continuidad de una función

¿Qué es la continuidad de una función?

En matemáticas, la continuidad de una función es una propiedad fundamental que describe cómo se comporta la función en relación con los valores cercanos de su dominio. Así, una función se considera continua si no presenta saltos, puntos indefinidos o discontinuidades en su gráfica.

Más formalmente, una función f(x) se dice continua en un punto “a” si se cumplen tres condiciones:

El límite de f(x) cuando x se aproxima a “a” existe, es decir, los límites laterales en el punto “a” coinciden.

El valor de f(a) está definido.

El límite de f(x) cuando x se aproxima a “a” es igual a f(a).

Simplificando, una función es continua si su gráfica puede dibujarse sin levantar el lápiz, es decir, no tiene agujeros, saltos o interrupciones. Esto implica que la función no tiene discontinuidades abruptas en su gráfica y que los valores de la función se acercan gradualmente a medida que los valores de x se acercan.

¿Cuál es la relación entre el dominio y la continuidad de una función?

El dominio de una función y su continuidad están estrechamente relacionados, pues para que una función sea continua en un punto, ese punto debe pertenecer al dominio de la función. Si un punto está excluido del dominio de la función, no se puede evaluar y, por lo tanto, no tiene sentido hablar de su continuidad en ese punto.

¿Cómo obtener la continuidad de una función?

Para determinar la continuidad de una función en un punto “a”, puedes seguir los siguientes pasos:

Verificar si la función está definida en el punto de interés: Comprueba si el valor de x en el punto dado está dentro del dominio de la función. Si la función no está definida en ese punto, no se puede hablar de continuidad en ese punto.

Evaluar los límites laterales: Calcula el límite de la función cuando x se aproxima al punto de interés desde la izquierda y desde la derecha. Si ambos límites laterales existen y son iguales, es decir, si los límites laterales coinciden, se cumple la primera condición para la continuidad.

Evaluar el valor de la función en el punto: Comprueba si el valor de la función en el punto de interés está definido. Si no está definido, la función no es continua en ese punto.

Comparar el límite con el valor de la función: Verifica si el límite de la función cuando x se acerca al punto de interés es igual al valor de la función en ese punto. Si ambos valores coinciden, se cumple la tercera condición para la continuidad.

Si todos estos pasos se cumplen, entonces la función es continua en el punto “a”.

Para determinar si la función es continua en todo su dominio, debes repetir estos pasos para cada punto dentro del dominio. Como estudiar la continuidad en infinitos puntos es materialmente imposible, para estudiar la continuidad en el dominio de una función debemos aprender reglas para las diferentes funciones para saber directamente en qué puntos podemos o no encontrar discontinuidades, y estudiar solo estos puntos. 

¿Se puede calcular la continuidad sin hacer los limites laterales?

No, para determinar la continuidad de una función en un punto específico x=a, es necesario calcular los límites laterales.

¿Qué tipos de discontinuidades hay?

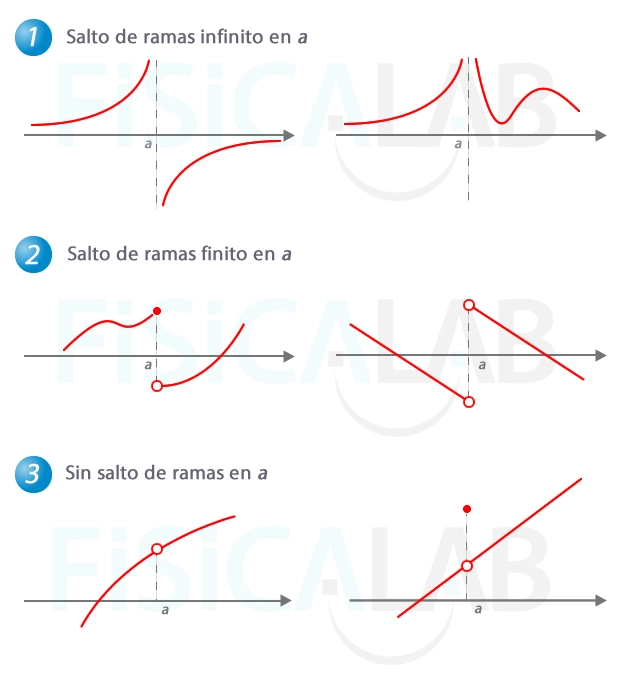
Cada tipo de discontinuidad implica un comportamiento particular en un punto o en un conjunto de puntos de una función, siendo los principales tipos los siguientes:

Discontinuidad evitable o punto removible: Ocurre cuando la función tiene un agujero o un hueco en un punto específico, pero se puede “rellenar” o corregir asignando un valor adecuado en ese punto. Matemáticamente, esto ocurre cuando los límites laterales coinciden, pero el valor de la función en el punto no.

Discontinuidad inevitable de salto finito: Ocurre cuando la función tiene un salto abrupto en un punto. En este tipo de discontinuidad, los límites laterales existen en el punto, pero no son iguales, provocando una interrupción o salto en la gráfica de la función.

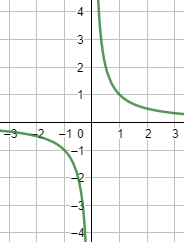
Discontinuidad inevitable de salto infinito: Ocurre cuando la función tiene al menos un límite lateral infinito o menos infinito en un punto. Esto genera una discontinuidad vertical en la gráfica de la función y una posterior asíntota vertical.

Es importante tener en cuenta que, en la práctica, las funciones pueden tener combinaciones de estos tipos de discontinuidades y pueden presentar comportamientos más complicados. 

Propiedades de las funciones continuas

Las operaciones algebraicas (suma, resta, multiplicación) de funciones continuas también resultan en funciones continuas. Por ejemplo, cada término individual en un polinomio es una función continua.

La multiplicación de una función continua por una constante también resulta en una función continua, pues la constante puede verse como una función continua en sí misma. 

La composición de funciones continuas también es continua.

¿Cuál es la continuidad de una función polinómica?

Las funciones polinómicas son ejemplos de funciones continuas, ya que son suma de monomios dados por una constante multiplicada por x elevado a una cierta potencia, luego es la suma de funciones continuas. Además, como el dominio de un polinomio es toda la recta real, estos son continuos en todos los puntos de R.

¿Cuál es la continuidad de una función racional?

La continuidad de una función racional, f(x) = P(x) / Q(x), donde P(x) y Q(x) son polinomios y Q(x); depende de su dominio y de los puntos en los que pueda haber discontinuidades, debiendo distinguir dos situaciones:

Discontinuidades evitables: Si el denominador Q(x) tiene raíces comunes con el numerador P(x), es posible que se produzcan discontinuidades evitables en los puntos donde el numerador y el denominador se anulen simultáneamente. Estos puntos de anulación pueden generar agujeros o huecos en la gráfica de la función. 

Discontinuidades inevitables de salto infinito: Si el denominador Q(x) tiene raíces que no son compartidas por el numerador P(x), se generarán discontinuidades no evitables de salto infinito, denotadas gráficamente por asíntotas verticales en dichos puntos.

¿Cuál es la continuidad de una función radical?

La continuidad de una función radical, f(x) = g(x)^(1/n), donde g(x) es una función continua y n es un número natural; depende del índice de la raíz (n), el radicando (g(x)) y el dominio de la función. 

Si el índice de la función es par, el dominio será solo los números para los que g(x) es positiva, luego la función será continua en dicho intervalo. Si el índice de la función es impar, el dominio será toda la recta real, y la función radical será continua en R.

¿Cuál es la continuidad de una función sinusoidal?

La continuidad de una función sinusoidal, f(x) = A*sin(g(x)), donde A es una constante; depende de la función en su argumento g(x). Asumiendo que ésta es continua, entonces como su dominio son todos los números reales, la función sinusoidal es una función continua en R.

¿Cuál es la continuidad de una función exponencial?

La continuidad de una función exponencial, f(x) = a^g(x), donde "a" es una constante positiva; depende de la función en su argumento g(x). Asumiendo que ésta es continua, entonces como su dominio son todos los números reales, la función sinusoidal es una función continua en R.

¿Cuál es la continuidad de una función logarítmica? 

La continuidad de una función logarítmica, f(x) = log_a(g(x)), donde "a" es la base del logaritmo; depende de su dominio y de las propiedades del logaritmo, pues su dominio son solo los valores de x para los que g(x)>0. De esta forma, si g(x) es continua en dicho intervalo, la función logarítmica también lo será.

¿Para qué sirve conocer la continuidad de una función?

Conocer la continuidad de una función es fundamental en el análisis y estudio de funciones matemáticas, ya que proporciona información valiosa sobre su comportamiento y propiedades en diferentes puntos y rangos de su dominio:

Análisis del comportamiento local: La continuidad de una función en un intervalo nos permite analizar su comportamiento local en ese intervalo. Si una función es continua en un intervalo, podemos examinar su tendencia, cambios de signo, existencia de máximos y mínimos locales, y otros aspectos relevantes.

Graficación: La continuidad de una función tiene un impacto directo en la apariencia de su gráfica. Una función continua muestra una curva suave y sin quiebres, mientras que las discontinuidades generan saltos, agujeros o comportamientos irregulares en la gráfica. Conocer la continuidad de una función nos ayuda a trazar su gráfica de manera más precisa y a comprender su forma general.

Aplicaciones en problemas reales: Muchos problemas en ciencias, ingeniería, economía y otras disciplinas se pueden modelar y resolver mediante funciones matemáticas. La continuidad de una función en el contexto de un problema real es esencial para asegurar que el modelo sea válido y que las soluciones obtenidas sean significativas y coherentes con la situación planteada.

Teoremas y propiedades: En el análisis matemático, existen teoremas y propiedades que se basan en la continuidad de una función, como pueden ser el teorema de Bolzano, el del valor intermedio o el del valor medio. Estos teoremas y propiedades proporcionan herramientas poderosas para resolver problemas y demostrar resultados importantes.

Derivación e integración: si una función no es continua en un punto dado, entonces no podemos calcular su derivada en dicho punto. Además, tampoco podemos calcular su integral en un intervalo que contenga al punto de discontinuidad. Por ende, la continuidad es una condición necesaria muy importante para calcular rectas tangentes y área por debajo de funciones.

Seguir aprendiendo:

1- La inteligencia artificial chat GPT

2- ¿Quieres ser una gran científica? 

3- Llévate el éxito

4- Dominio de una función

5- Puntos de corte con los ejes