Problema de los tres servicios

07-09-2023

¿Alguna vez habéis jugado a unir tres casas con tres servicios con líneas que no se crucen? Este antiguo acertijo es una simplificación para niños (y no tan niños) de uno de los problemas más típicos de la teoría de grafos, una rama de las matemáticas y las ciencias de la computación que estudia las propiedades de los grafos.

¿Qué es el problema de los tres servicios?

El problema de los tres servicios y las tres casas se plantea de la siguiente manera:

Supongamos que hay tres casas (A, B, C) y tres servicios (agua, gas y electricidad). El objetivo es encontrar una manera de conectar cada casa con cada servicio, de manera que no haya conexiones directas entre casas o servicios. Por ejemplo, la casa A no puede estar directamente conectada con la casa B, pero si pueden estar conectadas a través de un servicio. Además, y más importante, las conexiones entre casas y servicios no pueden intersecarse. El desafío consiste en encontrar una forma de realizar estas conexiones respetando las restricciones mencionadas, para lo que se va a plantear matemáticamente el problema gracias a la teoría de grafos y se va a obtener su solución, si es que la hay.

¿Qué es un grafo?

De manera general, un grafo es una estructura matemática que consta de un conjunto de elementos llamados “vértices” o “nodos”, y un conjunto de conexiones entre ellos llamadas “aristas”. Esto es, un grafo es cualquier objeto que se pueda imaginar con puntos conectados o no por líneas, y se utilizan para representar y estudiar relaciones entre objetos.

Formalmente, un grafo se define como un par ordenado G = (V, E), donde V es un conjunto no vacío de vértices y E es un conjunto de aristas que puede ser vacío, es decir, los puntos pueden no estar conectados. Cabe destacar que el grado de un vértice es el número de aristas que inciden en él. Los vértices de un grafo pueden representar entidades individuales, como ciudades, personas o conceptos, y las aristas representan las relaciones entre estas entidades. Por ejemplo, en un grafo que representa una red social, los vértices pueden representar usuarios y las aristas pueden representar amistades o interacciones entre ellos.

Existen diferentes tipos de grafos según sus propiedades y características:

Grafo dirigido: En este tipo de grafo, las aristas tienen una dirección específica. Si hay una arista que va del vértice A al vértice B, no necesariamente hay una arista que vaya de B a A. Además, si existen las dos entonces no son iguales.

Grafo no dirigido: En este tipo de grafo, las aristas no tienen una dirección específica. Si hay una arista que conecta el vértice A con el vértice B, también hay una arista que conecta B con A y son la misma. El que aquí estamos considerando es de este tipo.

Grafo bipartito: Es un grafo cuyos vértices se pueden dividir en dos conjuntos disjuntos, de manera que todas las aristas conectan vértices de un conjunto con vértices del otro.

Grafo cíclico: Es un grafo que contiene uno o más ciclos, es decir, una secuencia de aristas que permite recorrer un camino cerrado y regresar al mismo vértice. Este tipo de grafos tienen propiedades muy especiales.

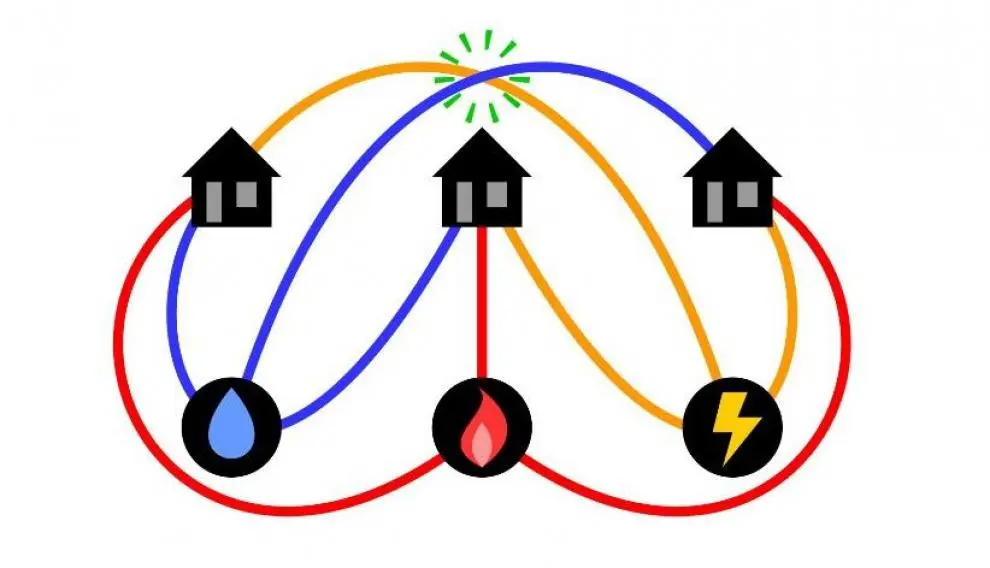
¿Qué es y cuáles son las propiedades de un grafo bipartito?

De los tipos de grafos mencionados antes hay uno en especial que se necesita comprender para resolver el acertijo: el grafo bipartito.

Un grafo bipartito es un tipo especial de grafo que debe cumplir las siguientes propiedades:

Se divide en dos conjuntos de vértices que no comparten elementos (disjuntos), llamémoslos U y V, de tal manera que cada arista del grafo conecte un vértice en U con un vértice en V.

No pueden existir aristas entre vértices del mismo conjunto, es decir, todas las aristas del grafo atraviesan la partición entre los dos conjuntos.

Además de etas, para un grafo bipartito se pueden desarrollar las siguientes propiedades:

Ciclos de longitud impar: Un grafo bipartito no puede contener ciclos de longitud impar, es decir, un conjunto de aristas que conecten un número impar de aristas que conecten vértices saliendo de uno y llegando al mismo. Esto se debe a que, en un ciclo de longitud impar, los vértices se alternarían entre los dos conjuntos, lo cual contradice la definición de grafo bipartito. Un ciclo sí puede ser par, conectando tantas veces como se quiera dos puntos, cada uno de un conjunto.

Conectividad: Un grafo bipartito puede tener diferentes niveles de conectividad. Algunos grafos bipartitos pueden ser conexos, lo que significa que hay un camino entre cada par de vértices. Otros pueden ser disconexos y tener componentes aislados, es decir, vértices sin conectar.

Los grafos bipartitos son utilizados en diversas áreas, como la teoría de redes, la planificación de horarios, la asignación de recursos y la teoría de juegos. Se pueden aplicar al emparejamiento de elementos, como estudiantes con escuelas o pacientes con médicos, y en problemas de asignación de tareas en los que se desea asignar elementos de un conjunto a elementos de otro de manera óptima. Dentro de los grafos bipartitos hay un subconjunto especialmente importante, que es el que se considera en el acertijo: los grafos bipartitos completos.

Los grafos bipartitos completos son grafos en los que todos los vértices del conjunto U están conectados a todos los vértices del otro conjunto V. También se conoce como grafo bipartito completamente conectado y se denota como K_(m,n), con m el número de vértices del conjunto U y n el número de vértices del conjunto V. La condición extra de ser un grafo completo impone algunas propiedades:

El grafo bipartito completo tiene un total de m + n vértices.

Cada vértice del conjunto U está conectado a todos los vértices del conjunto V, por lo que el número total de aristas es m * n, es decir, el producto del número de vértices en ambos conjuntos.

Todos los vértices de un mismo conjunto tienen el mismo grado, pues cada vértice del conjunto U tiene grado n, ya que está conectado a todos los vértices del conjunto V, y cada vértice del conjunto derecho tiene grado m.

Un grafo bipartito completo es conexo, lo que significa que hay una sola componente conexa que contiene todos los vértices. Esto quiere decir que no hay puntos aislados y que siempre se puede llegar de un vértice cualquiera a mediante las aristas.

¿Qué es y cuáles son las propiedades de un grafo plano?

Además de los grafos bipartitos, es necesario controlar el concepto de grafo plano. Un grafo plano es un tipo de grafo que se puede dibujar en un plano sin que existan cruces entre sus aristas, es decir, no tiene aristas que se intersequen en el plano. Además, en este tipo de grafos el grado de cada vértice debe ser mayor o igual a 3. La teoría de grafos planos ha podido obtener dos teoremas fundamentales que han permitido (y permiten) demostrar muchos resultados distintos: la fórmula de Euler y el teorema de Kuratowski.

La fórmula de Euler indica que, si un grafo plano es conexo, es decir, todos los vértices están conectados entre sí (sin bucles ni múltiples aristas) entonces se cumple la fórmula de Euler:

V - E + F = 2, donde V es el número de vértices, E el de aristas y F el de caras. Este es un teorema de que tiene una gran importancia en los cuerpos geométricos.

Por otro lado, el teorema de Kuratowski establece que un grafo es plano si y solo si no contiene un subgrafo homeomorfo al grafo completo K_5 (un grafo con 5 vértices conectados entre sí) ni al grafo bipartito completo K_(3,3) (un grafo bipartito con 3 vértices en un conjunto y 3 vértices en otro conjunto, y todas las posibles conexiones entre los dos conjuntos). Este último teorema quiere decir que un grafo es plano si no contiene otro grafo dentro de él que sea un grafo bipartito completo con dos conjuntos de al menos 3 elementos cada uno, ni otro grafo dentro que tenga al menos 5 vértices conectados todos entre sí.

Y, entonces, ¿cómo se resuelve el problema de los tres servicios?

El problema de los tres servicios y las tres casas que antes hemos descrito se puede modelizar por un grafo bipartito completo (hay dos conjuntos disjuntos de vértices, las casas y los servicios) con tres elementos cada uno. Además, es un grafo bipartito por no poder unirse dos casas o dos servicios directamente, y es completo porque cada casa debe estar unida a todos los servicios y viceversa. La búsqueda de la solución matemáticamente consiste en plantearse si este grafo es plano, es decir, si puede dibujarse sin que haya cruces entre las aristas (las uniones entre casas y servicios).

Finalmente, podemos deducir que, por el teorema de Kuratowski, este grafo no es plano, pues es en sí mismo el grafo K_(3,3), que no es plano. Esto es, el acertijo/problema no tiene solución si se dibuja como una figura plana, es decir, en un papel (en tres dimensiones sí tendría solución). Así, no se pueden conectar tres casas con tres servicios sin que al menos dos de las líneas que representan las conexiones se crucen.