¿Qué es el producto vectorial?

El producto vectorial, también conocido como producto cruz, es una operación entre dos vectores que produce un nuevo vector perpendicular a ambos. Se trata entonces de una operación que relaciona un espacio vectorial consigo mismo, pues el vector obtenido pertenece al mismo espacio vectorial y es único, es decir, el producto vectorial de dos vectores es un único vector. 

No es una operación invertible, pues dos pares de vectores distintos pueden dar el mismo vector al hacer su producto vectorial.

El producto vectorial se denota con el símbolo "×" o con el símbolo “∧”, para evitar confusiones con la letra x.

¿Cuál es la diferencia entre el producto vectorial y el producto escalar?

El producto vectorial y el producto escalar son dos operaciones diferentes entre vectores. La clave entre ellos está en lo que se obtiene de ellos:

El producto escalar, también conocido como producto punto, es una operación entre dos vectores que produce un número escalar.

El producto vectorial es una operación entre dos vectores que produce un nuevo vector perpendicular a ambos. 

¿Cuándo se puede hacer un producto vectorial?

El producto vectorial se puede hacer cuando se tienen dos vectores en un espacio tridimensional. Es decir, los vectores deben tener tres componentes (x, y, z) para poder calcular el producto vectorial. Esto es así porque en otras dimensiones la definición de producto vectorial no tiene sentido:

En un espacio bidimensional no se podría definir un vector perpendicular a otros dos, pues ese vector se saldría del plano que se está considerando. 

En espacios con dimensiones superiores (dimensión d), el vector perpendicular a otros dos no sería único, estaría de hecho contenida en una figura de dimensión d-2 que es perpendicular a los dos vectores.

¿Cuáles son las propiedades producto vectorial?

Las propiedades más importantes son:

Distributividad: El producto vectorial es distributivo sobre la suma. Esto significa que: 

A×(B+C) = (A×B)+(A×C)

Anticonmutatividad: El producto vectorial inverso es el opuesto del producto vectorial. Esto significa que: A×B=-(B×A)

Producto vectorial de vectores ortogonales: El producto vectorial de dos vectores perpendiculares es igual al producto del módulo de los vectores multiplicado por un vector unitario en la dirección perpendicular al plano formado por los vectores.

A × B = |A||B|un, 

donde un es un vector unitario perpendicular a A y B, y su dirección está determinada por la regla de la mano derecha.

No distributividad del producto consigo mismo:  A×(B×C)≠(A×B)×C. 

De hecho, se cumple la identidad de Jacobi:

A×(B×C)+C×(A×B)+B×(C×A) =0

¿Cómo se calcula el producto vectorial de dos vectores?

El producto vectorial de dos vectores A y B en tres dimensiones se puede calcular con matrices utilizando la siguiente fórmula del determinante:

A × B = det(R, A, B)

Donde R es el vector (i, j, k) que indica las direcciones, pues i, j, k son los vectores unitarios de los ejes X, Y, Z.

Así, se debe resolver el determinante:

Esto también puede escribirse directamente como:

A × B = (AyBz - AzBy, AzBx – AxBz, AxBy – AyBx)

Donde Ax, Ay, Az y Bx, By, Bz son las componentes de los vectores A y B.

Por ejemplo, si tenemos los vectores A = (2, 1, -3) y B = (4, -2, 1), el producto vectorial se puede calcular como sigue:

Así, se sigue que directamente del determinante se obtiene: (-5i - 14j - 8k)

Este vector equivale al que se obtendría con la fórmula:

A×B = (1·1 - (-3)·(-2), (-3)·4 – 2·1, 2·(-2) – 1·4) =  (-5, -14, -8)

Por lo tanto, el resultado del producto vectorial de A y B es el vector (-5, 14, -8). El módulo del producto vectorial es simplemente el módulo de este vector:

|A×B| = sqrt((-5)^2+(-14)^2+(-8)^2) = sqrt(285)

Por otro lado, existe una relación directa para calcular el módulo del producto vectorial mediante el módulo (norma) de los vectores y el ángulo que forman:

|A×B| = |A||B|sin(θ)

De esta forma, si solo nos interesa el módulo del producto vectorial, es decir, el módulo (o norma) del vector que se obtiene al realizar el producto vectorial, podemos emplear esta relación.

Por ejemplo, si tenemos que los vectores cumplen |A| = 2 y |B| = 1, y el ángulo que forman es 30º, entonces se tendrá que el módulo de su producto vectorial es:

|A×B| = |A||B|sin(θ) = 2·1·sin(30º) = 1

En definitiva, en función de lo que queramos conseguir y de los datos de los que dispongamos usaremos un método o el otro. 

¿Cómo se calcula el producto vectorial de tres vectores?

El producto vectorial de tres vectores, o doble producto vectorial,se puede escribir en función de otros dos productos vectoriales, aplicando la identidad de Jacobi y la no distributividad: 

A×(B×C)+B×(C×A) = -C×(A×B) 

Esto se puede reescribir como: (A×B)×C = A×(B×C)+(C×A)×B

Aun así, la identidad más interesante es la que relaciona el producto vectorial en función de dos productos escalares:

(A×B)×C = (A·C)B–(B·C)A

El doble producto vectorial es, de nuevo, un vector, que es perpendicular a los tres vectores empleados. Así, si los tres vectores son perpendiculares, entonces el doble producto vectorial es cero.

¿Cuándo el producto vectorial de dos vectores es 0?

Si dos vectores son paralelos o coincidentes, es decir, si tienen un ángulo de 0 grados entre ellos, su producto vectorial es igual a cero. Esto se deduce directamente de su fórmula, pues el sen de 90º es 0, siendo entonces que:

A×B = |A||B| sin(0º) = 0

Esto lleva a que el producto vectorial de un vector por sí mismo es: A × A = 0

Interpretación geométrica del producto vectorial

La interpretación geométrica del producto vectorial es la que da la definición: el resultado del producto vectorial es un nuevo vector que es perpendicular al plano que contiene los dos vectores originales. 

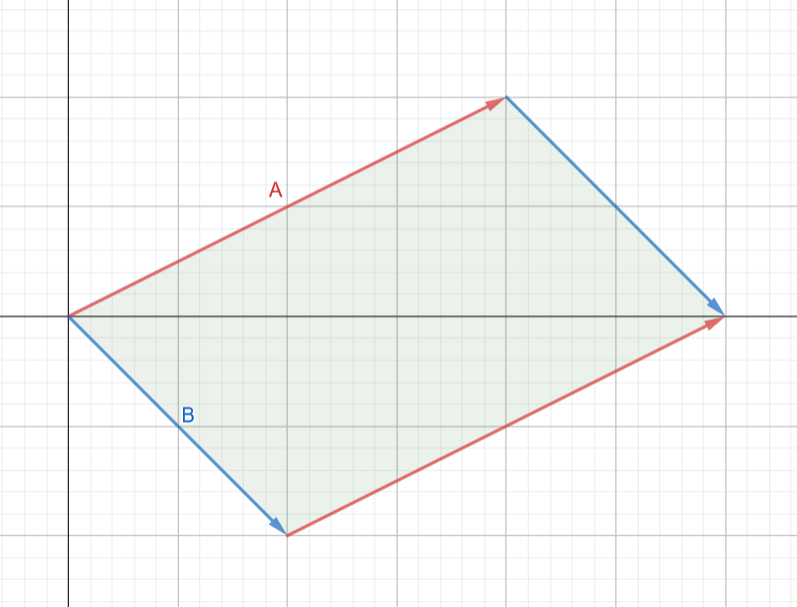
Además, el producto vectorial es muy útil porque el módulo del vector resultante es igual al área del paralelogramo que se forma con los dos vectores originales. Es decir, si tenemos dos vectores A y B, y realizamos su producto vectorial A × B, el resultado será un nuevo vector C, que es perpendicular al plano que contiene a A y a B. 

La dirección del vector C está dada por la regla de la mano derecha, es decir, si se coloca A en el dedo índica y B en el dedo corazón, la dirección de A × B la indica el dedo pulgar. 

¿Qué es el producto mixto de tres vectores?

El producto mixto, también conocido como triple producto escalar, es una operación matemática que se aplica a tres vectores en el espacio tridimensional. El resultado del producto mixto es un número escalar, y se define como el producto escalar de un producto vectorial, es decir, es un producto que combina los dos anteriores.

El producto mixto se denota como A · (B × C), donde A, B y C son vectores en el espacio tridimensional, "·" representa el producto escalar (punto), que es una operación que devuelve un número escalar, y "×" representa el producto vectorial (cruz), que es una operación que devuelve un vector. 

¿Cómo se calcula el producto mixto de tres vectores?

El producto mixto de tres vectores A, B y C se puede expresar como un determinante de una matriz de 3x3. La matriz se construye utilizando los vectores A, B y C como columnas (o como filas, el resultado es el mismo), pero colocándolos en el orden en que se hagan:

A·(B×C) = det(A, B, C)

La fórmula para el determinante de una matriz de 3x3 se puede obtener en función de las coordenadas de los vectores:

det([A, B, C]) = Ax·(ByCz-BzCy)+Ay·(BzCx-BxCz)+Az·(BxCy-ByCx)

Donde Ax, Ay y Az son las componentes del vector A, e igual para B y C.

Propiedades del producto mixto

Las propiedades más importantes del producto mixto son:

Propiedad conmutativa: El producto mixto es conmutativo con respecto al producto escalar, lo que significa que no importa el orden en que se realice. Es decir:

(A×B)·C = C·(A×B)

Propiedad distributiva: El producto mixto también es distributivo con respecto a la suma de vectores. Esto es: (A×B)·(C+D) = (A×B)·C+(A×B)·D

Propiedad cíclica: si se permutan los vectores que están “al lado” en el producto mixto dos veces (permutación par), el resultado no cambia. Es decir:

(A×B)·C = (B×C)·A = (C×A)·B

Propiedad de inversión: Si se invierten los vectores, es decir, se permutan los vectores que están “al lado” en el producto mixto una vez, el resultado únicamente cambia de signo. Es decir:

(A×B)·C = -(B×A)·C = -(A×B)·C

Interpretación geométrica del producto mixto

La interpretación geométrica del producto mixto es que el escalar obtenido (en valor absoluto) representa el volumen de un paralelepípedo definido por tres vectores en el espacio tridimensional. Así, el módulo del producto vectorial corresponde al área de la base del paralelepípedo y el tercer vector es equivalente a la altura.

Si no se considera el valor absoluto del escalar obtenido se pueden considerar tres casos:

Si el producto mixto es positivo, entonces los vectores A, B y C definen un paralelepípedo con volumen positivo. 

Si el producto mixto es negativo, entonces el volumen es negativo, lo que significa que los vectores A, B y C definen un paralelepípedo con la orientación opuesta. 

Si el producto mixto es cero, entonces los vectores A, B y C son coplanares, lo que significa que los tres vectores se encuentran en un mismo plano.

Para seguir aprendiendo:

1- La inteligencia artificial ya esta aquí y se llama chat GPT

2- ¿Quieres ser una gran científica? Estamos a tu lado

3- Llévate el éxito

4- Dominio de una función

5- Puntos de corte con los ejes